Skip to contents

PCA with penguins and recipes

Source: vignettes/pca.Rmd
pca.Rmd

You’ll need these packages to follow along with the code in this article locally:

Correlation matrix

The palmerpenguins::penguins data contains several size measurement variables that are correlated. Let’s take a look at the correlation matrix with the corrr package and the corrr::correlate() function:

library(corrr)
penguins_corr <- penguins %>%
  dplyr::select(body_mass_g, ends_with("_mm")) %>%
  correlate() %>%
  rearrange()
penguins_corr
#> # A tibble: 4 x 5
#>   rowname           flipper_length_mm body_mass_g bill_length_mm bill_depth_mm
#>   <chr>                         <dbl>       <dbl>          <dbl>         <dbl>
#> 1 flipper_length_mm            NA           0.871          0.656        -0.584
#> 2 body_mass_g                   0.871      NA              0.595        -0.472
#> 3 bill_length_mm                0.656       0.595         NA            -0.235
#> 4 bill_depth_mm                -0.584      -0.472         -0.235        NA

Body mass and flipper length appear highly correlated, but neither of the bill variables appears to be as highly correlated with any other variables.

Pairwise plot matrix

We can visualize these correlations with the GGally package. The function we’ll use is called GGally::ggpairs().

penguins %>%
  select(species, body_mass_g, ends_with("_mm")) %>% 
  GGally::ggpairs(aes(color = species),
          columns = c("flipper_length_mm", "body_mass_g", 
                      "bill_length_mm", "bill_depth_mm")) +
  scale_colour_manual(values = c("darkorange","purple","cyan4")) +
  scale_fill_manual(values = c("darkorange","purple","cyan4"))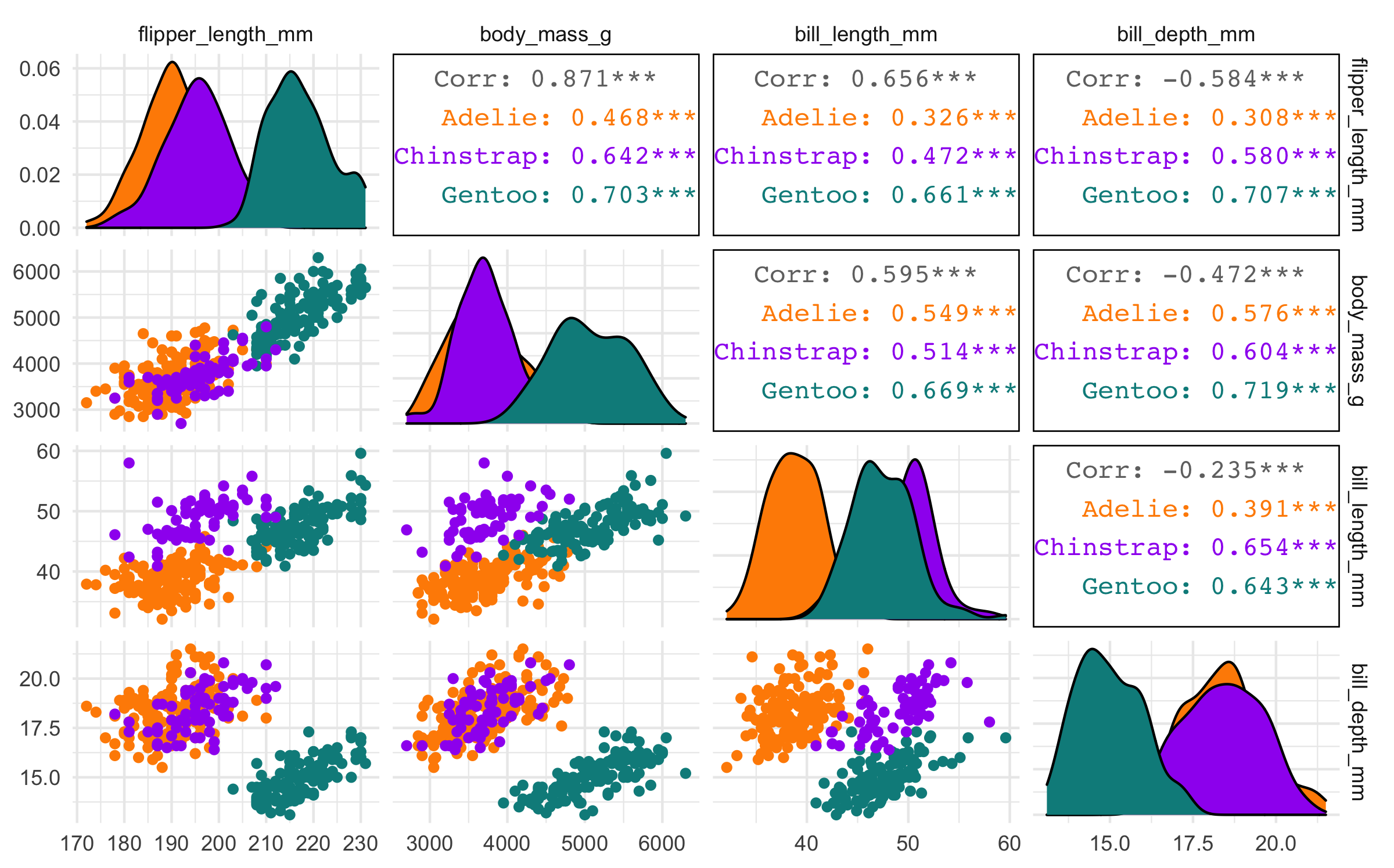

Principal component analysis (PCA)

We’ll use the recipes package from tidymodels to perform a principal component analysis (PCA).

First, we’ll also use a few recipe steps to preprocess the data for PCA; namely, we need to:

  • remove any NA values,
  • center all predictors, and
  • scale all predictors.

If you’ve never used the recipes package before, try this article to get started.

library(recipes)
penguin_recipe <-
  recipe(~., data = penguins) %>% 
  update_role(species, island, sex, year, new_role = "id") %>% 
  step_naomit(all_predictors()) %>% 
  step_normalize(all_predictors()) %>%
  step_pca(all_predictors(), id = "pca") %>% 
  prep()

penguin_pca <- 
  penguin_recipe %>% 
  tidy(id = "pca") 

penguin_pca
#> # A tibble: 16 × 4
#>    terms                value component id   
#>    <chr>                <dbl> <chr>     <chr>
#>  1 bill_length_mm     0.455   PC1       pca  
#>  2 bill_depth_mm     -0.400   PC1       pca  
#>  3 flipper_length_mm  0.576   PC1       pca  
#>  4 body_mass_g        0.548   PC1       pca  
#>  5 bill_length_mm    -0.597   PC2       pca  
#>  6 bill_depth_mm     -0.798   PC2       pca  
#>  7 flipper_length_mm -0.00228 PC2       pca  
#>  8 body_mass_g       -0.0844  PC2       pca  
#>  9 bill_length_mm    -0.644   PC3       pca  
#> 10 bill_depth_mm      0.418   PC3       pca  
#> 11 flipper_length_mm  0.232   PC3       pca  
#> 12 body_mass_g        0.597   PC3       pca  
#> 13 bill_length_mm     0.146   PC4       pca  
#> 14 bill_depth_mm     -0.168   PC4       pca  
#> 15 flipper_length_mm -0.784   PC4       pca  
#> 16 body_mass_g        0.580   PC4       pca

The value column here is the loading. For each component, the value tells us the linear combination of weights for each variable that contributes to that component.

This output is a tidy version of this using stats::prcomp():

penguins %>% 
  dplyr::select(body_mass_g, ends_with("_mm")) %>% 
  tidyr::drop_na() %>% 
  scale() %>% 
  prcomp() %>%  
  .$rotation
#>                          PC1         PC2        PC3        PC4
#> body_mass_g        0.5483502 0.084362920 -0.5966001 -0.5798821
#> bill_length_mm     0.4552503 0.597031143  0.6443012 -0.1455231
#> bill_depth_mm     -0.4003347 0.797766572 -0.4184272  0.1679860
#> flipper_length_mm  0.5760133 0.002282201 -0.2320840  0.7837987

We can also apply the recipes::tidy() method to the output from recipes::step_pca() to examine how much variance each component accounts for:

penguin_recipe %>% 
  tidy(id = "pca", type = "variance") %>% 
  dplyr::filter(terms == "percent variance") %>% 
  ggplot(aes(x = component, y = value)) + 
  geom_col(fill = "#b6dfe2") + 
  xlim(c(0, 5)) + 
  ylab("% of total variance")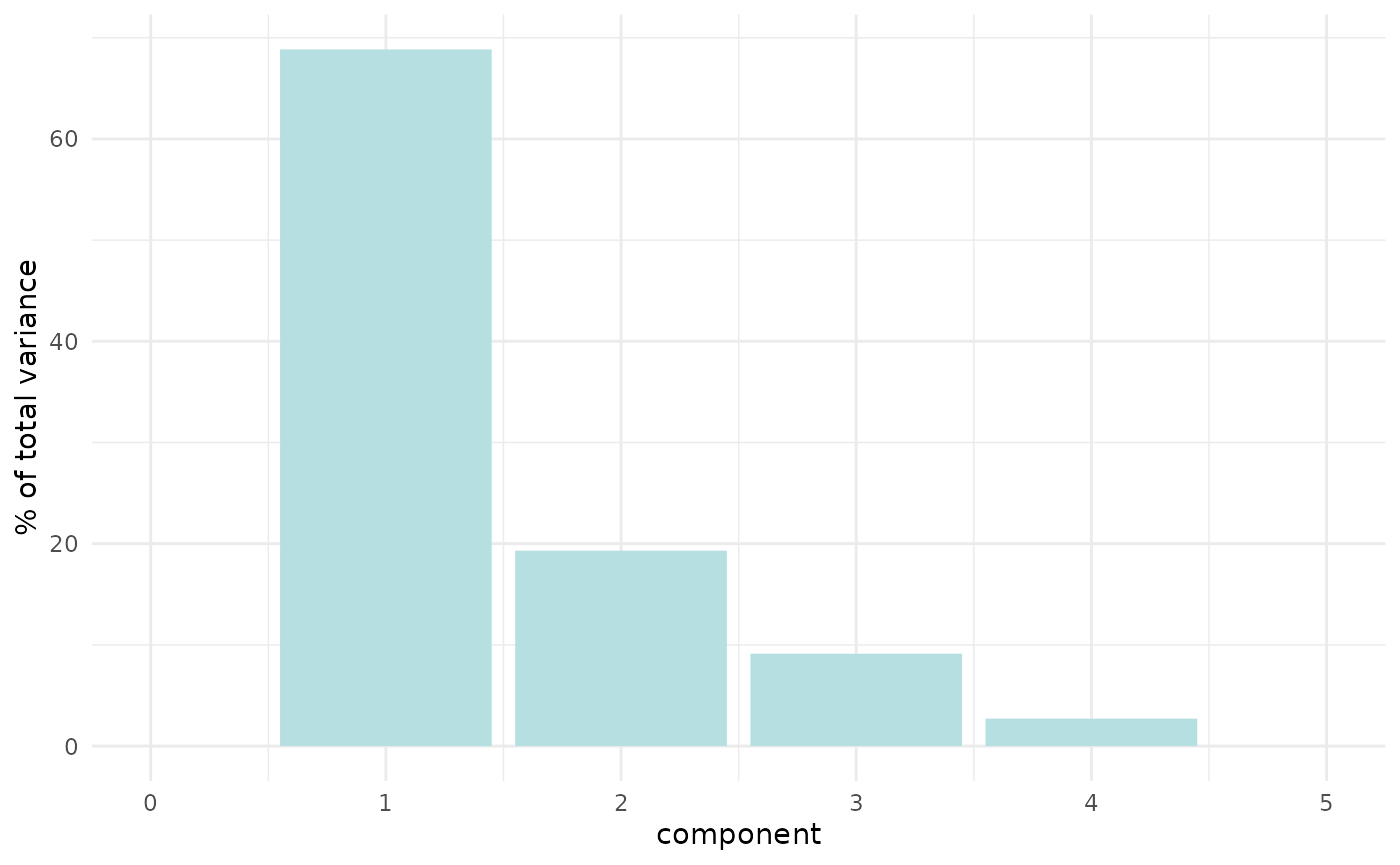

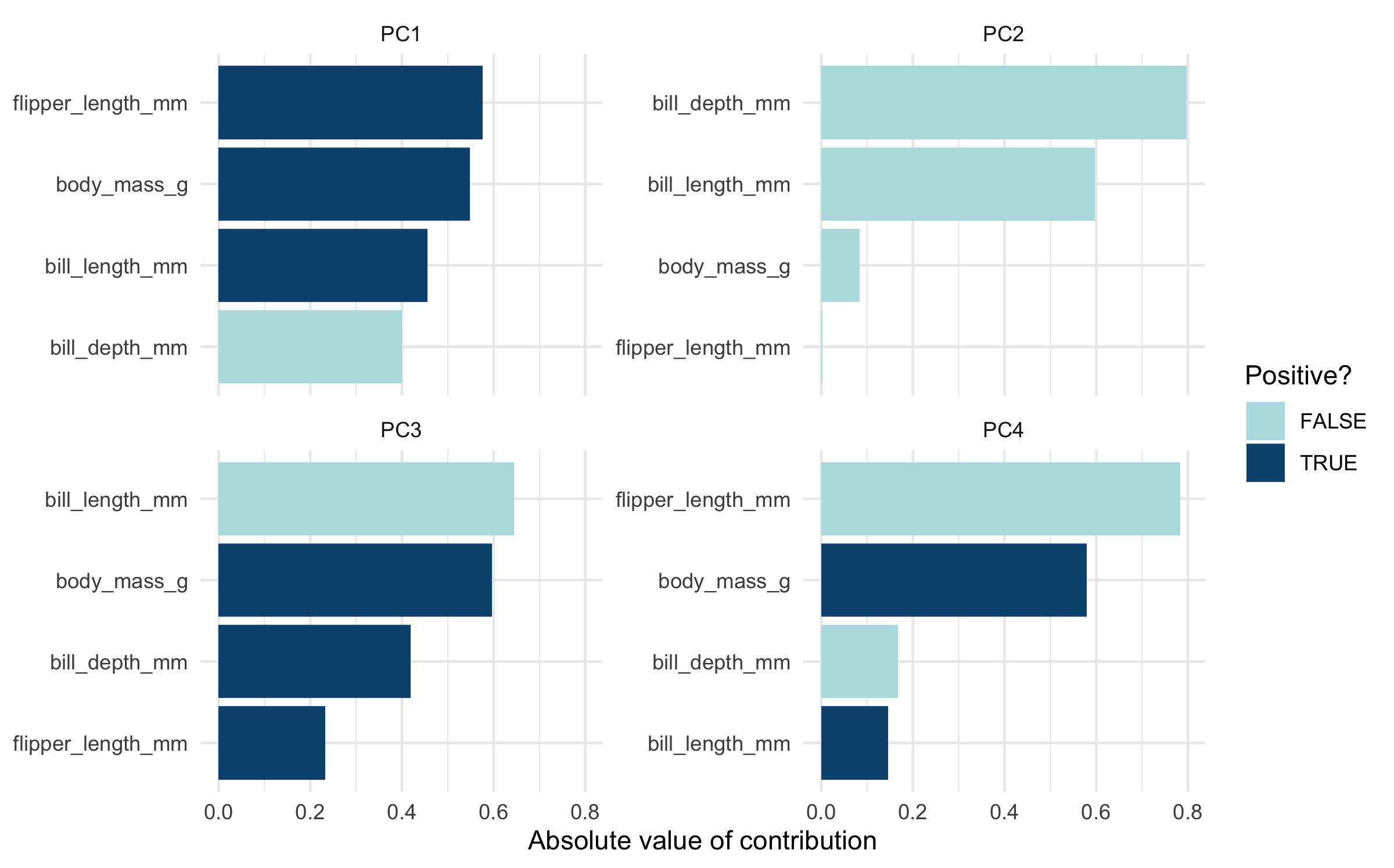
Plot PCA loadings

We can plot these loadings by principal component too, following Julia Silge’s example:

library(ggplot2)
penguin_pca %>%
  mutate(terms = tidytext::reorder_within(terms, 
                                          abs(value), 
                                          component)) %>%
  ggplot(aes(abs(value), terms, fill = value > 0)) +
  geom_col() +
  facet_wrap(~component, scales = "free_y") +
  tidytext::scale_y_reordered() +
  scale_fill_manual(values = c("#b6dfe2", "#0A537D")) +
  labs(
    x = "Absolute value of contribution",
    y = NULL, fill = "Positive?"
  )

Plot PCA loadings + scores

We have the PCA loadings in penguin_pca. But we need them in a wide format now for plotting.

# get pca loadings into wider format
pca_wider <- penguin_pca %>% 
  tidyr::pivot_wider(names_from = component, id_cols = terms)

We also need to go back to our prepped penguin recipe, prepped_penguins, and recipes::juice() it to get the PCA scores back.

# define arrow style
arrow_style <- arrow(length = unit(.05, "inches"),
                     type = "closed")


pca_plot <-
  juice(penguin_recipe) %>%
  ggplot(aes(PC1, PC2)) +
  geom_point(aes(color = species, shape = species), 
             alpha = 0.8, 
             size = 2) +
  scale_colour_manual(values = c("darkorange","purple","cyan4")) 

pca_plot +
  geom_segment(data = pca_wider,
               aes(xend = PC1, yend = PC2), 
               x = 0, 
               y = 0, 
               arrow = arrow_style) + 
  geom_text(data = pca_wider,
            aes(x = PC1, y = PC2, label = terms), 
            hjust = 0, 
            vjust = 1,
            size = 5, 
            color = '#0A537D')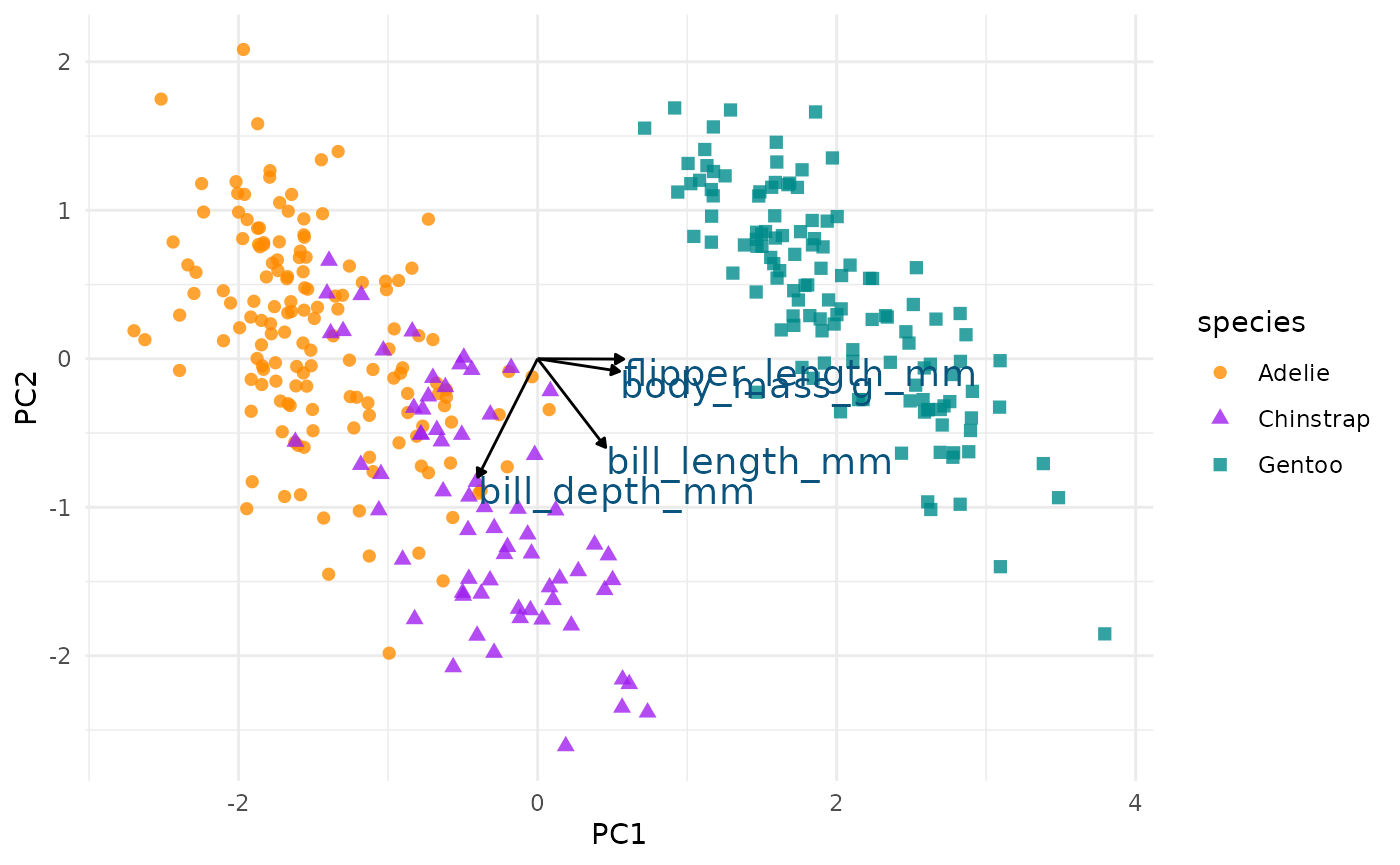

In the above plot, you can see a lot!

First, if you focus on the x-axis showing us the first principal component, you can see that flipper length and body mass are very important (confirming what we saw in the above bar chart). Along this dimension, Gentoo penguins stand out clearly from the other two species. We can confirm this looking at summary statistics:

penguins %>% 
  group_by(species) %>% 
  summarize(across(c(flipper_length_mm, body_mass_g), 
                   mean, 
                   na.rm = TRUE)) 
#> # A tibble: 3 × 3
#>   species   flipper_length_mm body_mass_g
#>   <fct>                 <dbl>       <dbl>
#> 1 Adelie                 190.       3701.
#> 2 Chinstrap              196.       3733.
#> 3 Gentoo                 217.       5076.

We can see this with a simple scatterplot:

ggplot(penguins, aes(x = flipper_length_mm, y = body_mass_g, colour = species)) +
  geom_point() +
  scale_colour_manual(values = c("darkorange","purple","cyan4"))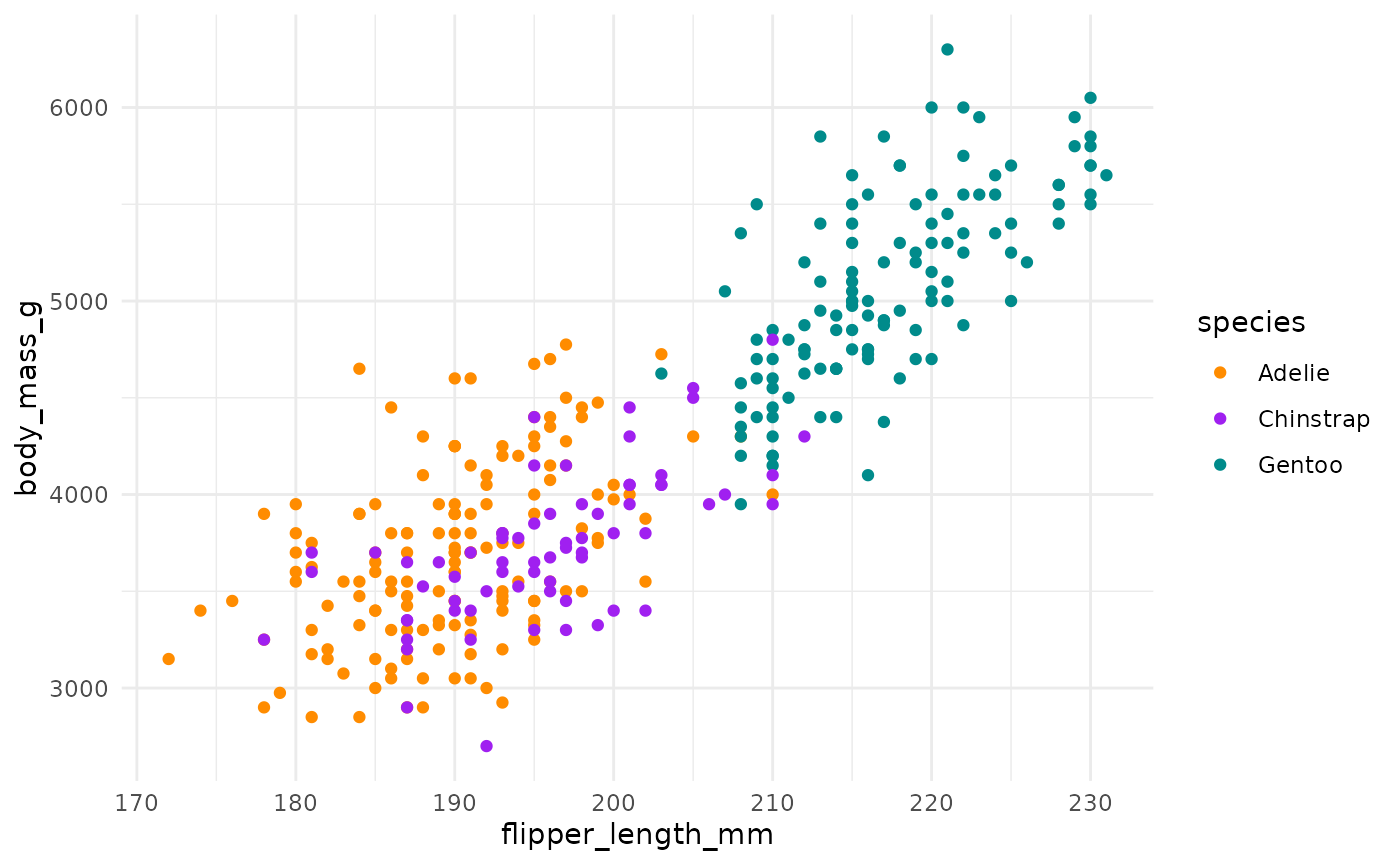

If you now focus more on the y-axis showing us the second principal component, you can see that our two bill size variables, bill_length_mm and bill_depth_mm, are very important (again, confirming what we saw in the above bar chart).

Let’s do the same thing for principal component 2 and 3.

pca_plot %+% 
  aes(PC2, PC3) +
  geom_segment(data = pca_wider,
               aes(xend = PC2, yend = PC3), 
               x = 0, 
               y = 0, 
               arrow = arrow_style) + 
  geom_text(data = pca_wider,
            aes(x = PC2, y = PC3, label = terms), 
            hjust = 0, 
            vjust = 1,
            size = 5, 
            color = '#0A537D')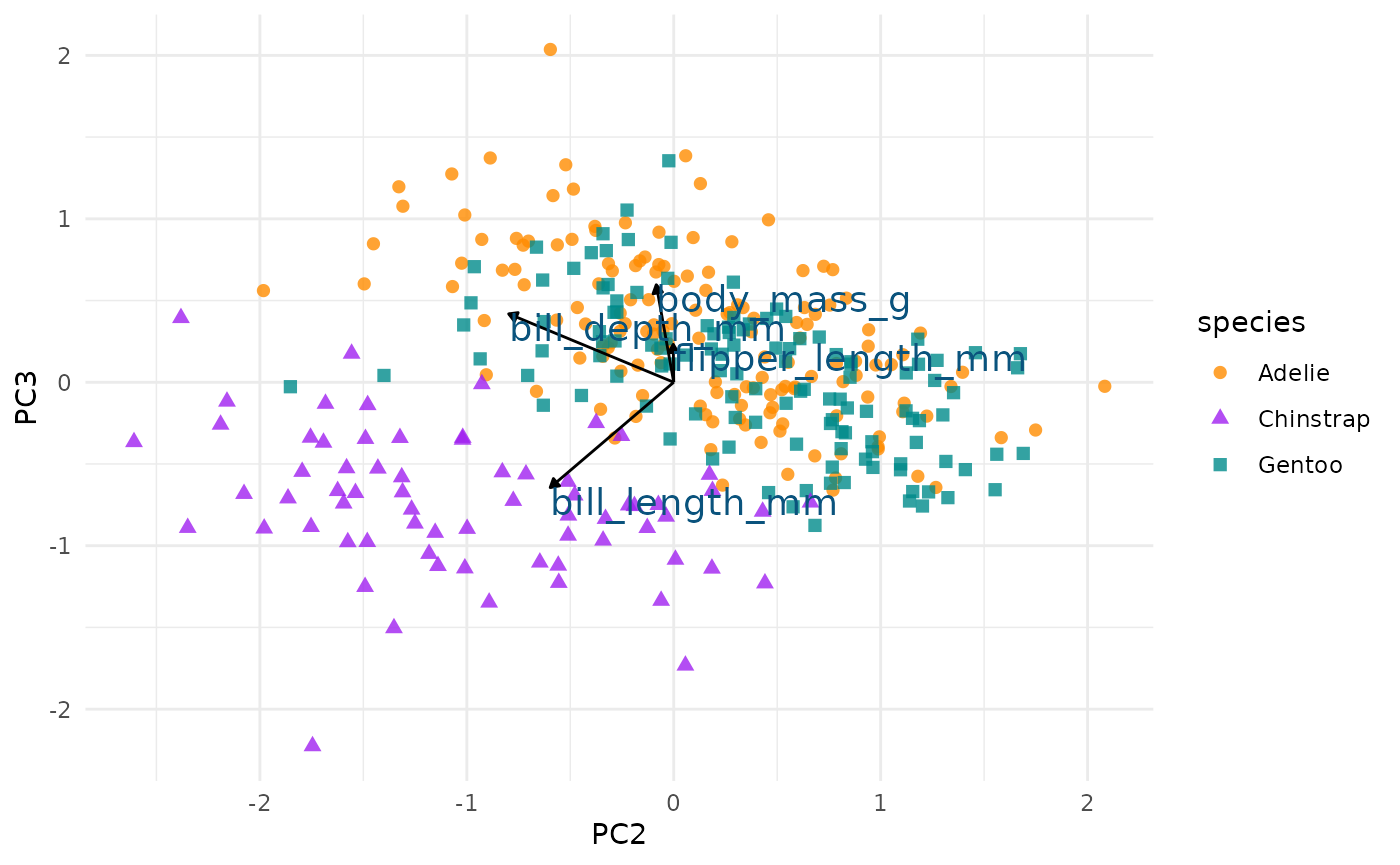

We see again that PC2 seems most associated with our bill size variables, bill_length_mm and bill_depth_mm. But now we can see more clearly that this dimension seems to separate Chinstrap penguins from the other two species. We can confirm this by glancing at summary statistics again by species:

penguins %>% 
  group_by(species) %>% 
  summarize(across(c(bill_depth_mm, bill_length_mm), 
                   mean, 
                   na.rm = TRUE))
#> # A tibble: 3 × 3
#>   species   bill_depth_mm bill_length_mm
#>   <fct>             <dbl>          <dbl>
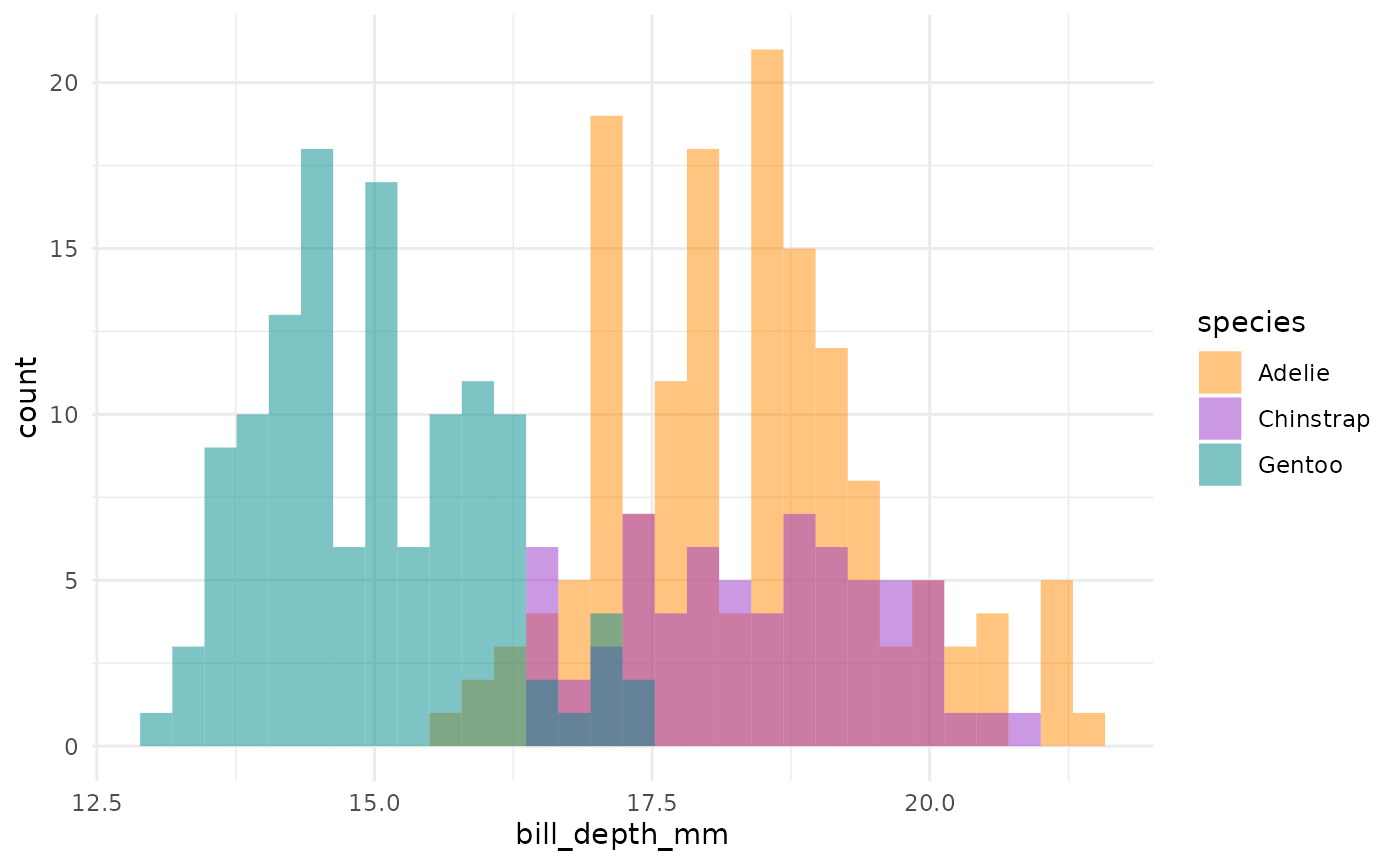
#> 1 Adelie             18.3           38.8
#> 2 Chinstrap          18.4           48.8
#> 3 Gentoo             15.0           47.5

We can see this with a simple scatterplot too:

ggplot(penguins, aes(x = bill_length_mm, y = bill_depth_mm, colour = species)) +
  geom_point() +
  scale_colour_manual(values = c("darkorange","purple","cyan4"))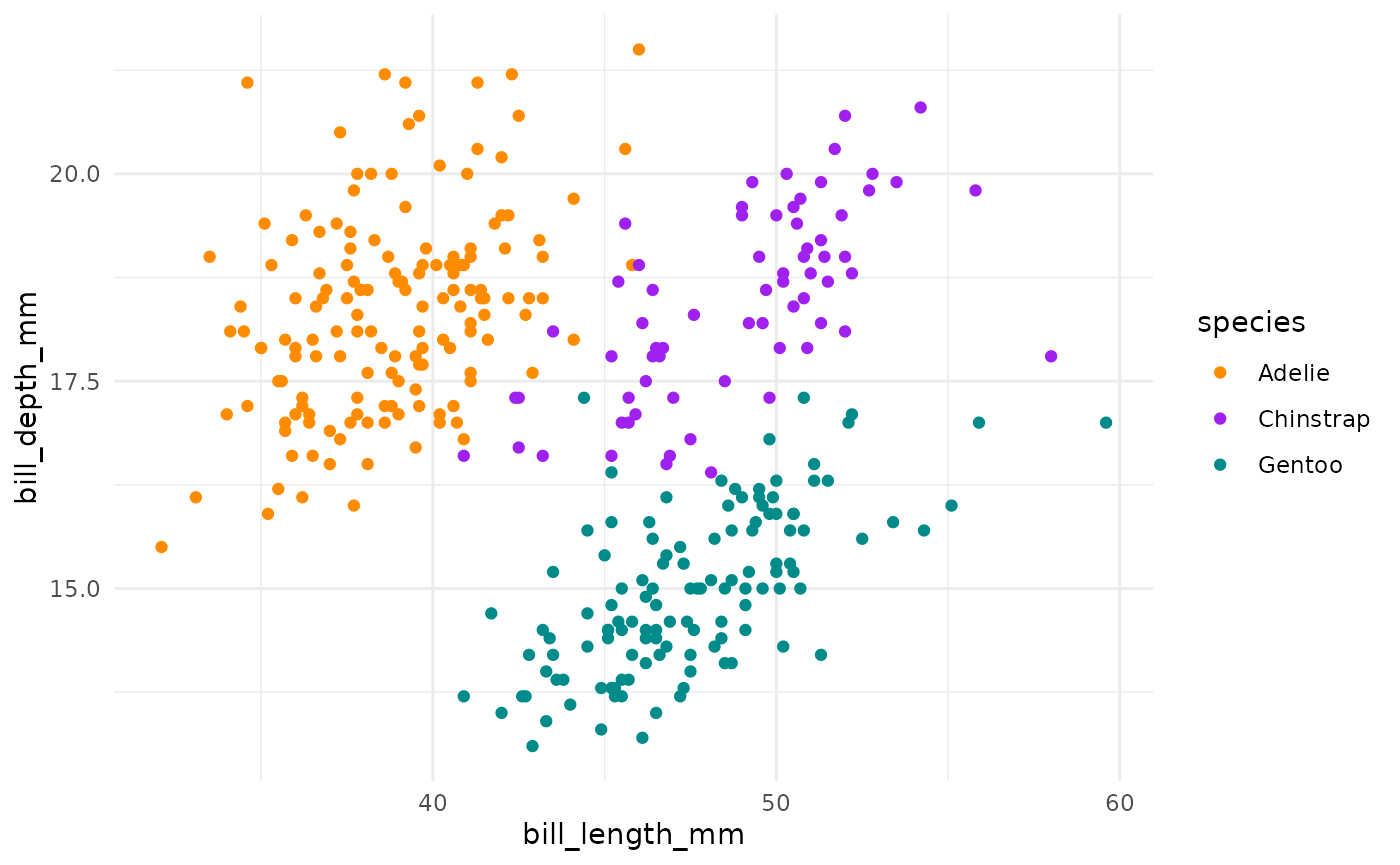

This is actually a pretty neat scatterplot—it highlights a perfect example of why you’d need the combination of two variables to differentiate between these three species. Comparing distributions for any single variable only differentiates one species from the other two!1

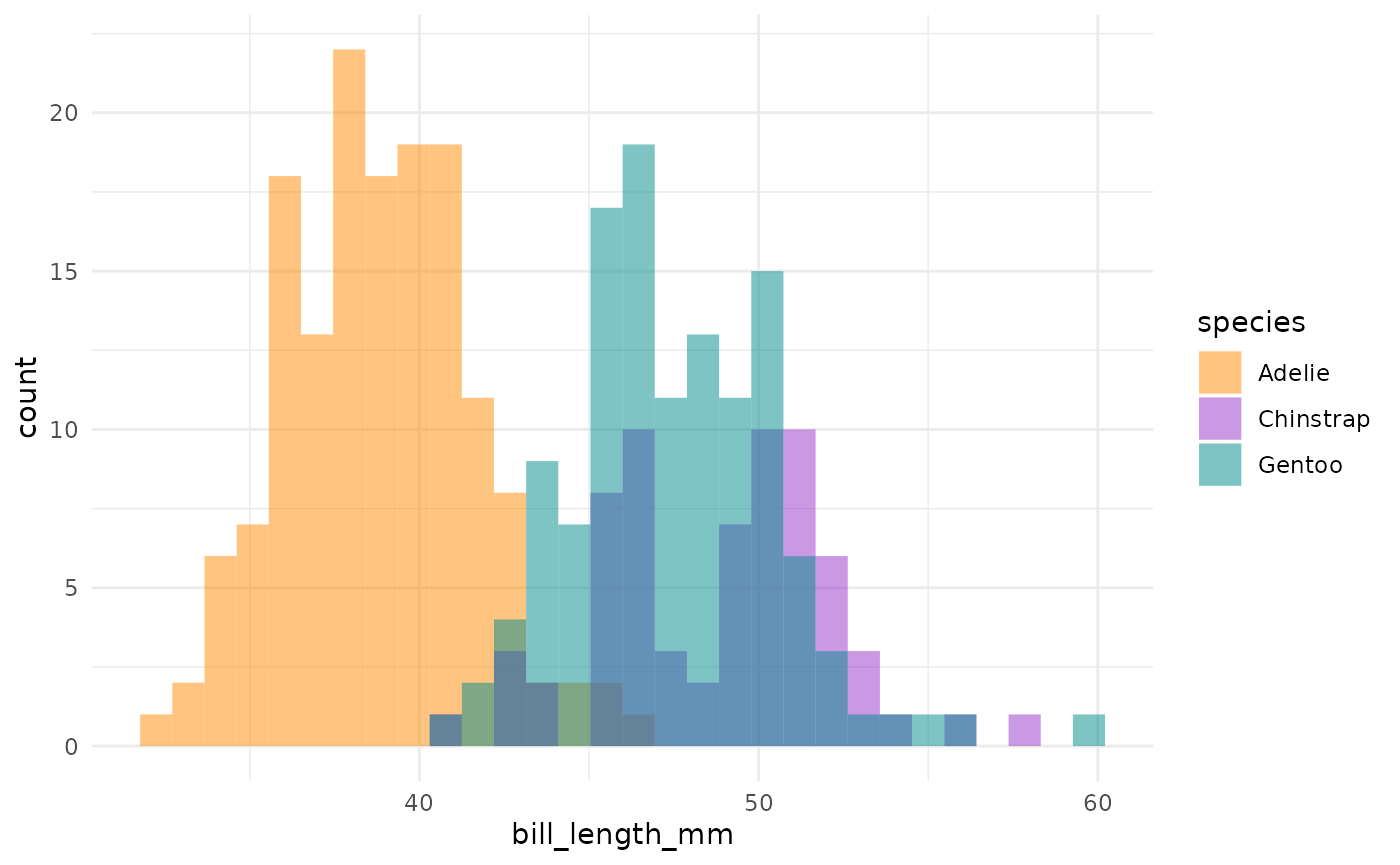
Summary

So, Gentoos appear to just be giants, compared to the Adelie and Chinstrap penguins. While Adelie and Chinstraps are similar size-wise as measured by flipper length and body mass, Chinstraps seem to have longer bills and Adelie penguins have stubbier bills (a pug-gein, if you will?). And Gentoos, despite being large overall, have flatter bills than either of the other two species. Reminder:

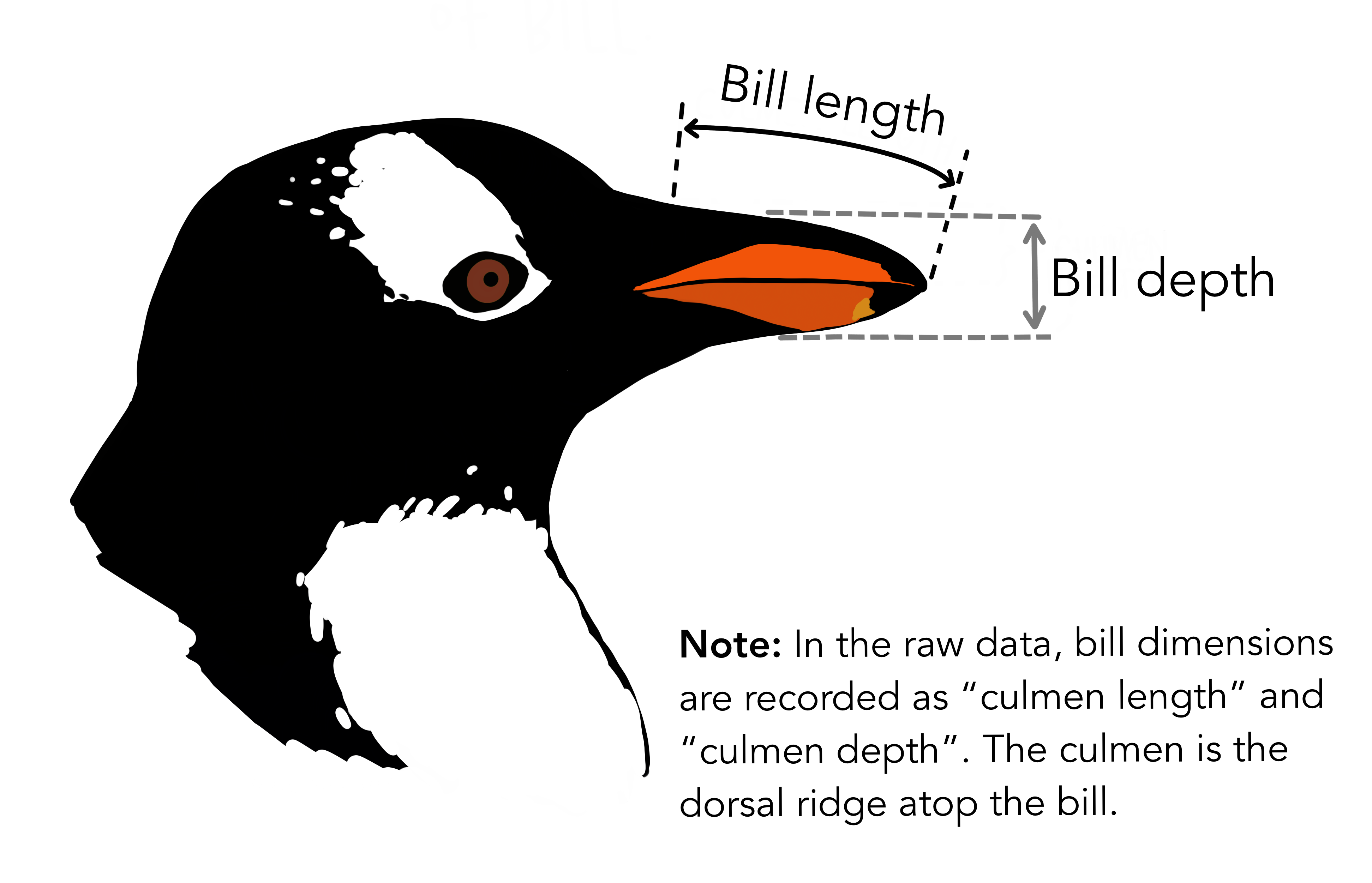
Other PCA resources