class: center, middle, inverse, title-slide # EDS 212 ## Day 2 Part 1: Definition of the derivative --- ## Overview of Day 2 topics - Derivatives - Higher order & partial derivatives - Differential equations (reading, understanding, solving, using) --- class: center, middle ## What if we want to find an expression that describes the rate of change (slope) at *any* point on a function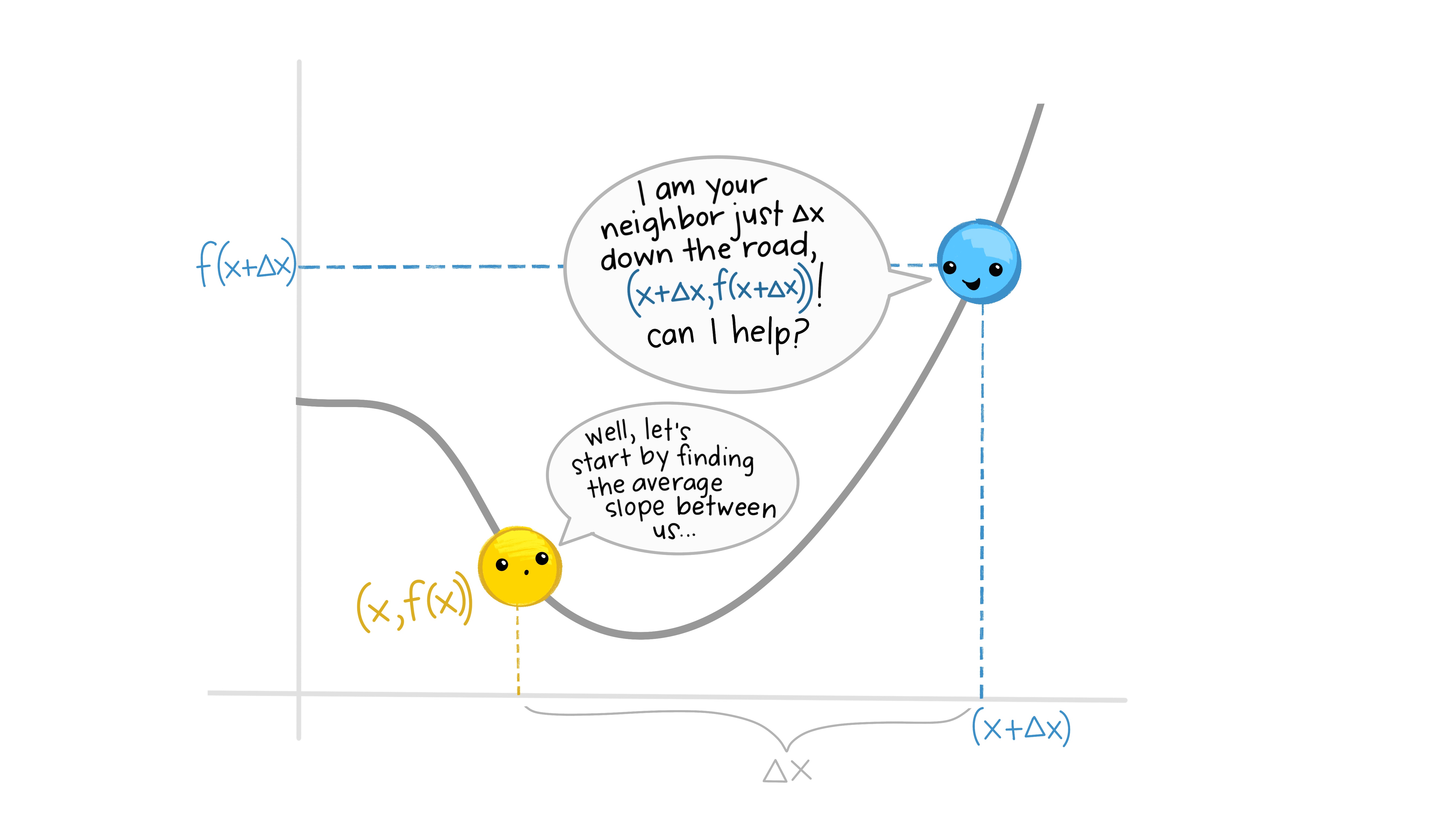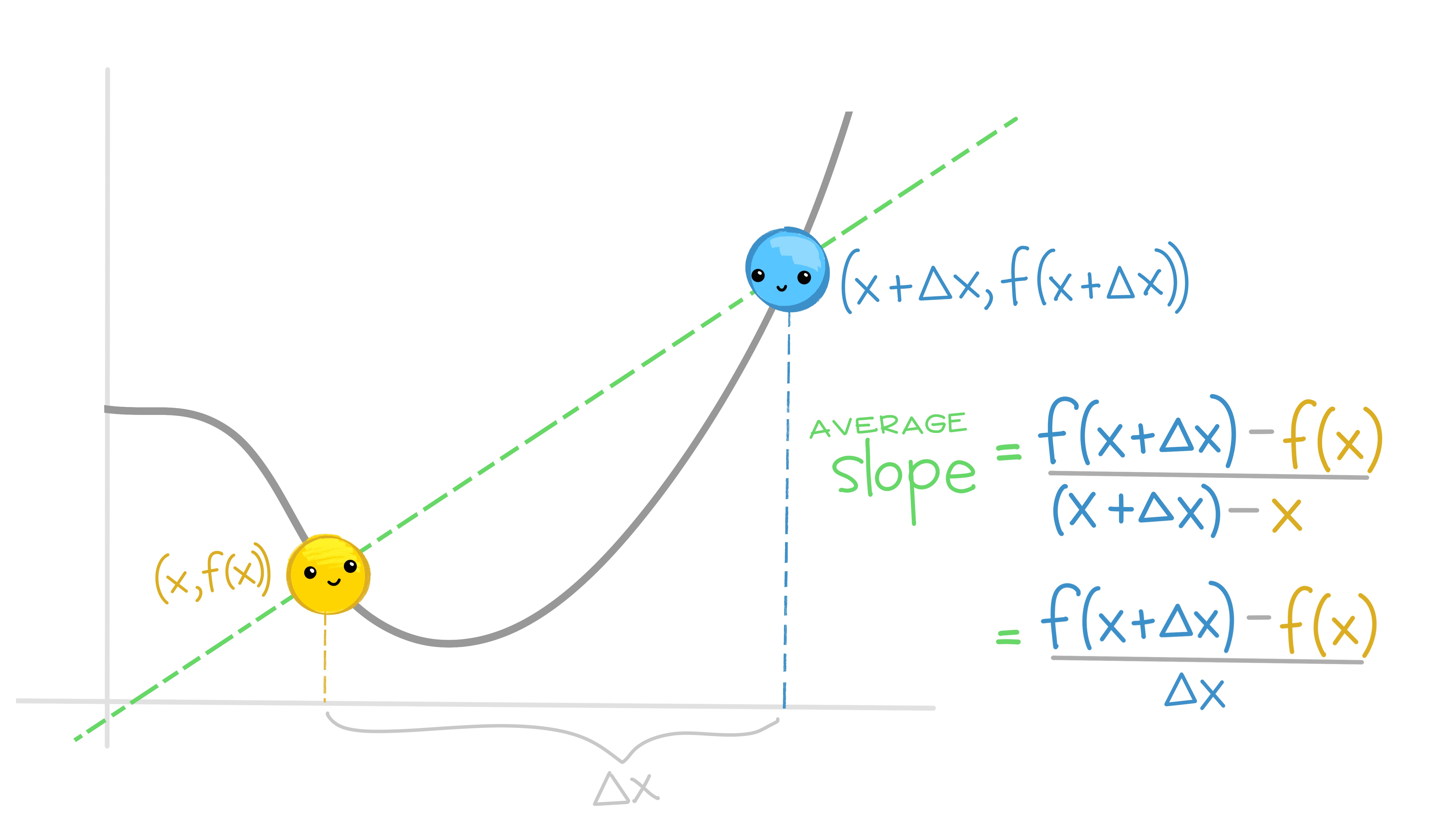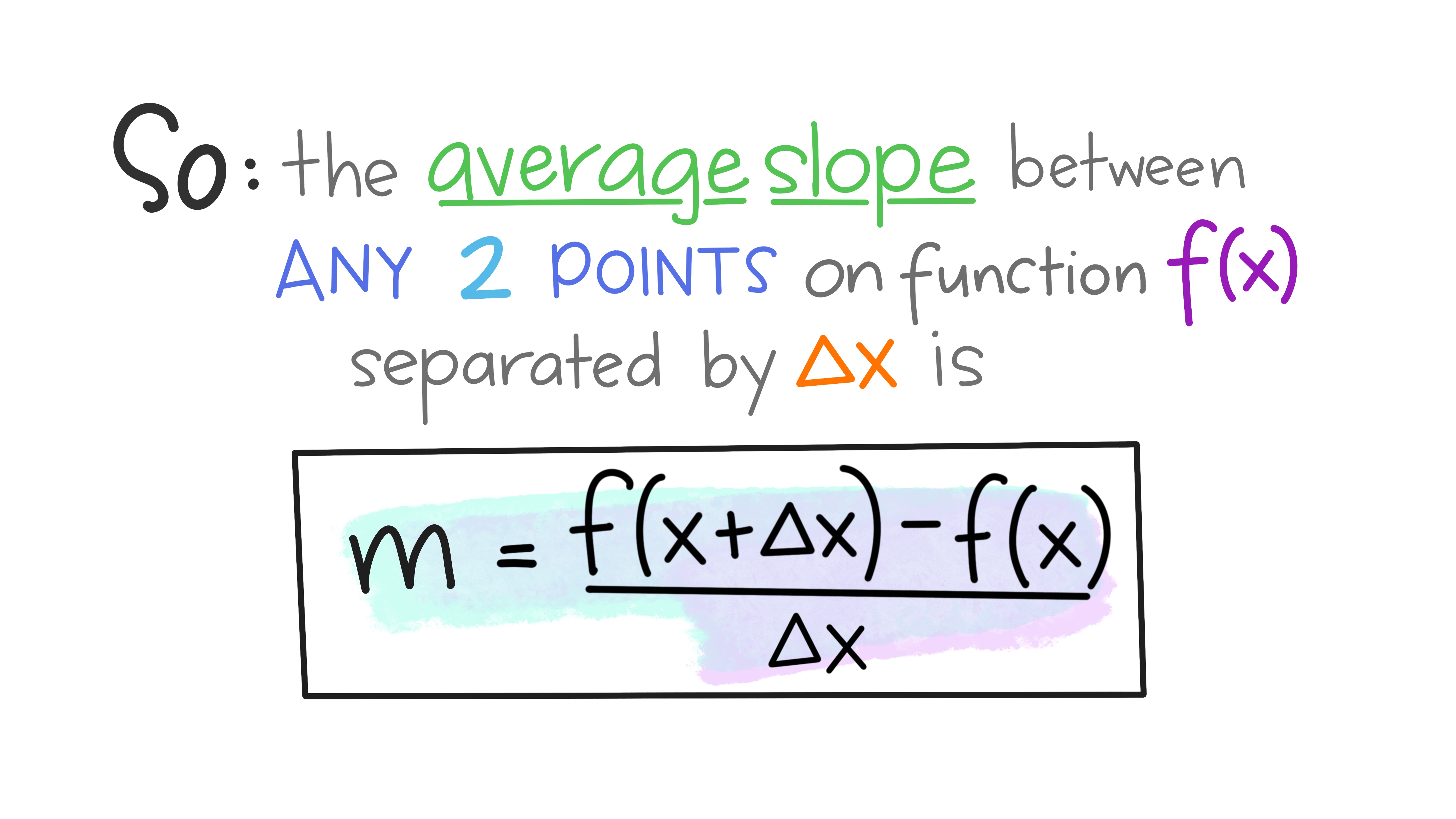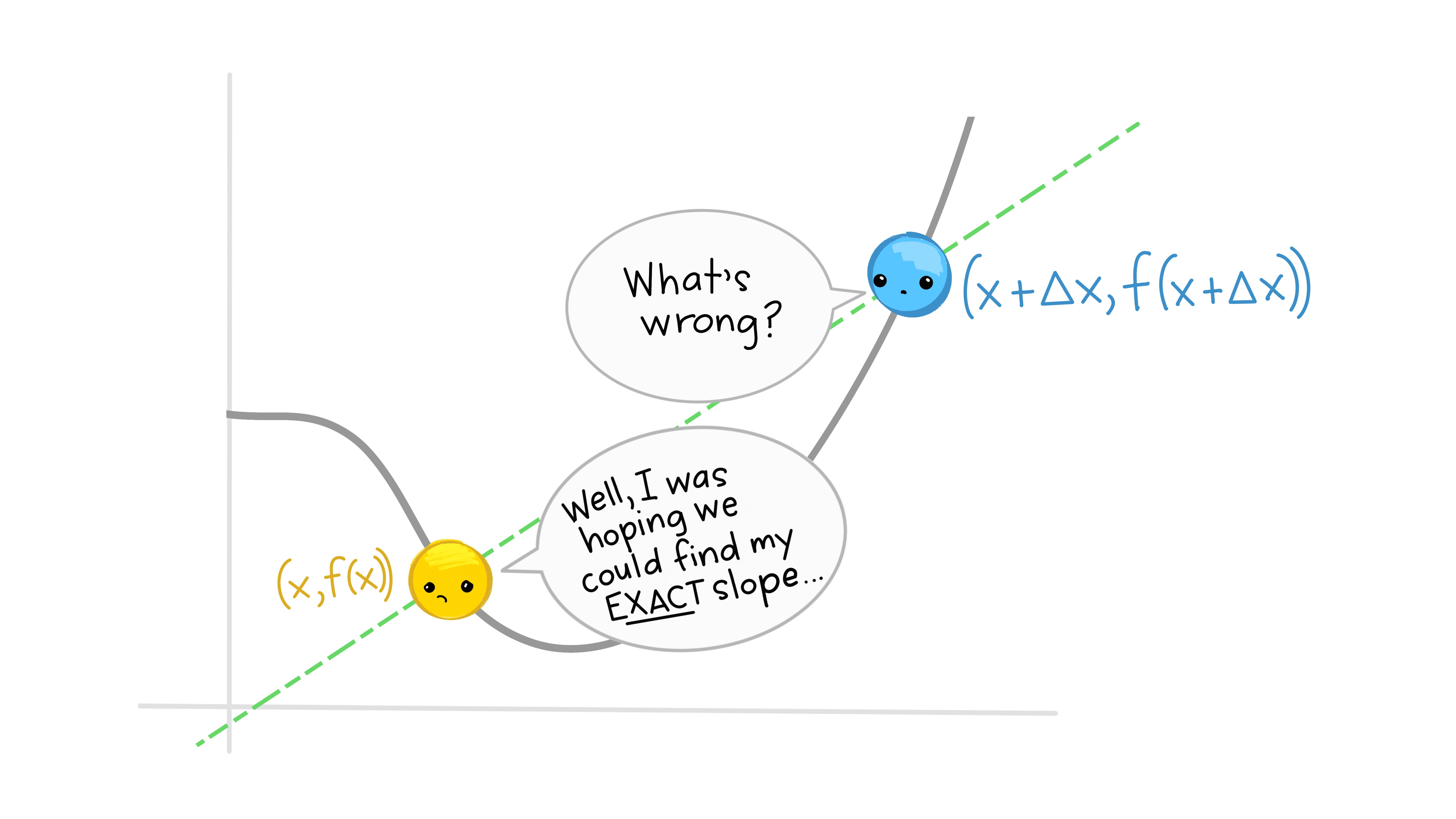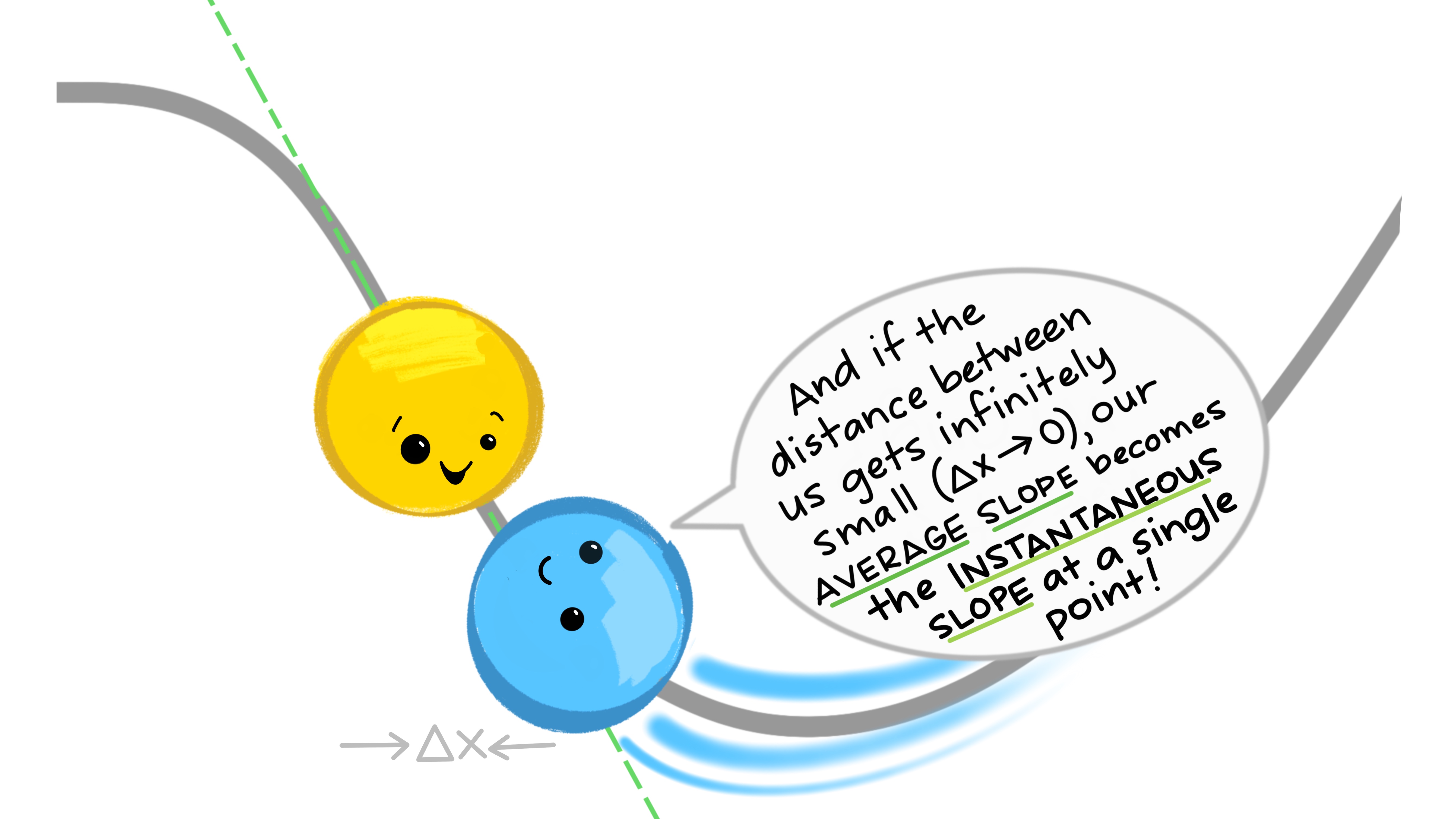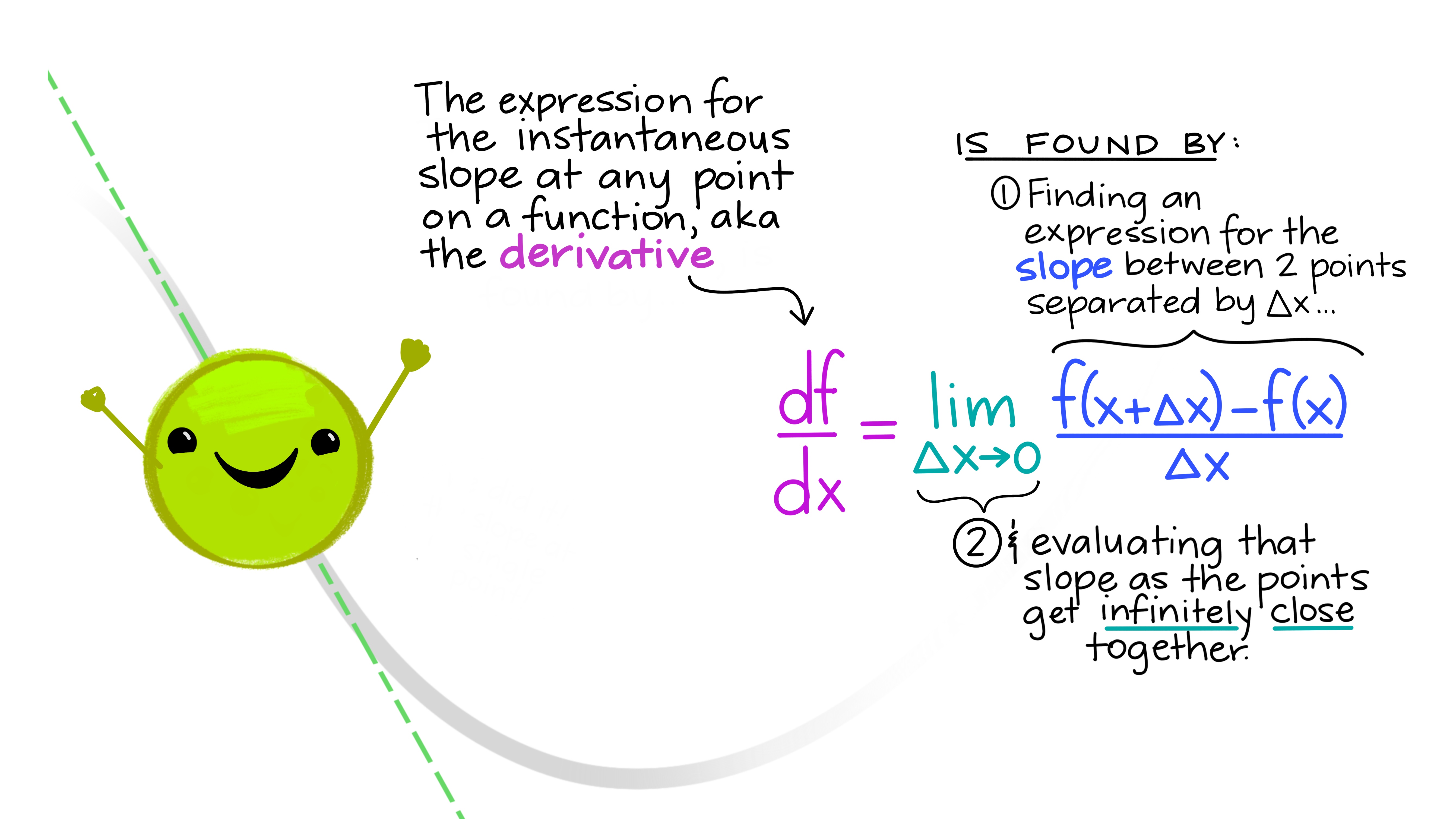? ---  ---  ---  ---  ---  ---  ---  ---  ---  --- ## And that's how we find derivatives Evaluate the slope between two generic points on any function (separated by `\(\Delta x\)`) as `\(\Delta x\)` becomes infinitely small. <img src="slide_images/mispronounced_equations.png" width="35%" style="display: block; margin: auto;" /> --- ### Let's try one. Find an expression that tells us the slope of the function `\(f(x)=x^2-18.2\)` at any value of `\(x\)`. `$$\frac{df}{dx}=\lim_{\Delta x\to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}$$` `$$=\lim_{\Delta x\to 0}\frac{((x+\Delta x)^2-18.2)-(x^2-18.2)}{\Delta x}$$` `$$=\frac{x^2+2x\Delta x+(\Delta x)^2-18.2-x^2+18.2}{\Delta x}$$` --- Which gets us to... `$$= \lim_{\Delta x\to 0} \frac{2x\Delta x+(\Delta x)^2}{\Delta x} = \lim_{\Delta x\to 0} {2x+\Delta x} = 2x$$` --- ## Your turn: Find the derivative of the following using the definition of the derivative: `$$f(x)=4-x+3x^2$$` --- ### It's cool to do that a few times, **but it gets really tedious really fast.** So we have some basic derivative shortcut rules to speed it up a bit: - **Power rule:** `\(\frac{d}{dx}(x^n)=nx^{n-1}\)` - **Constant rule:** if `\(k\)` is a constant, `\(\frac{d}{dx}(k)=0\)` - **Constant multiple rule:** if `\(k\)` is a constant, `\(\frac{d}{dx}(kx) = k\space\)` - **Sum and difference rule:** `\(\frac{d}{dx}(f(x)\pm g(x))=\frac{d}{dx} f(x)\pm \frac{d}{dx}g(x)\)` Yeah there are more - we're not doing them. --- **ALL** of those rules come from the definition of the derivative. <img src="slide_images/derivative_9.jpg" width="70%" /> --- class: center, middle ## Reminder of what we're doing mathematically: ### Finding the slope between two generic points on a function as the distance between them gets infinitely small. That will give us an expression for the **slope at any point on the original function**. --- ## Derivative of logs & exponents - `\(\frac{d}{dx}(e^x) = e^x\)` - `\(\frac{d}{dx}ln(x)=\frac{1}{x}\)`